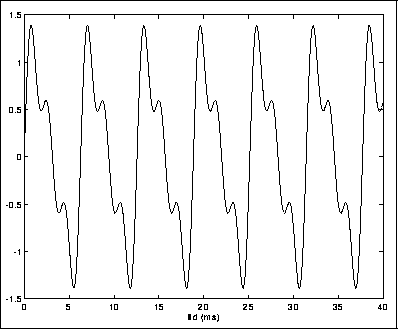
Figure 3.1: Statisk lyd
Ved å betrakte et oscillogram kan vi si endel om lydens egenskaper. Dersom vi har en statisk lyd, dvs. at den ikke endrer seg over måletidsrommet, kan oscillogrammet se ut f.eks. som i figur 3.1.
Tre grunnleggende parametre bestemmer hvordan en lyd oppfattes av øret: Amplityde, frekvens og klangfarge.
Amplityden er graden av utslag, og leses av som maksimalverdier i
oscillogrammet. Amplityden til lyden over er ca. 1.4.
Lydstyrken vi vil oppfatte avhenger av amplityden: Større amplityde
gir kraftigere lyd. Nå har det seg imidlertid slik at øret
oppfatter lydstyrke logaritmisk, slik at sammenhengen mellom lydstyrke
og amplityde ikke er lineær. Vi bruker derfor gjerne enheten
desi-Bel (etter Alexander Graham Bell) som mål for amplityde.
Når det gjelder akustisk lyd, går vi fram på følgende
måte. Først bestemmer vi oss for at den svakeste lyden vi kan
høre skal kalles 0 dB (dette er definert som ![]() for
en sinustone på 2 kHz). Amplityden til denne lyden kan vi kalle
for
en sinustone på 2 kHz). Amplityden til denne lyden kan vi kalle
![]() , fordi den brukes som en referanse som vi sammenlikner andre
amplityder med. En lyd med amplityde a har nå følgende styrke
målt i dB
, fordi den brukes som en referanse som vi sammenlikner andre
amplityder med. En lyd med amplityde a har nå følgende styrke
målt i dB
![]() :
:
![]()
Når vi benytter dB-skalaen, kan vi si endel kvantitative ting om hvordan øret oppfatter lydstyrke. Den minste endring i lydstyrke som vi kan merke er ca. 1 dB. Den kraftigste lyd vi kan høre uten at vi får vondt er på ca. 120 dB. Vi sier at ørets dynamiske område er 120 dB. Dette tilsvarer et amplityde-område på en million til en! Det er svært vanskelig å lage elektronikk som kan håndtere et så stort spenningsområde. Profesjonelt lydutstyr har oftest et dynamisk område på under 100 dB.
En viktig konsekvens for oss data-musikere er at vi ikke kan øke amplityden lineært og så regne med at vi får et naturlig crescendo. Vi må istedet bruke en eller annen eksponensiell funksjon.
I oscillogrammet over kan vi se en periodisitet; den samme kurveformen gjentar seg igjen og igjen. Slike lyder oppfattes som en kontinuerlig og ren tone. Antall gjentakelser pr. sekund gir frekvensen til den grunntonen vi oppfatter, målt i Hertz. Har vi en grunntone på f.eks. 110 Hz, betyr dette at den periodiske kurveformen gjentar seg selv 110 ganger i sekundet. Dersom vi dobler til 220 Hz, hører vi dette som et sprang en oktav opp. Videre dobling til 440 Hz gir enda en oktav. Dette innebærer at heller ikke sammenhengen mellom frekvens og oppfattet tonehøyde er lineær. Jo høyere vi går opp i registret, jo lengre avstand er det mellom halvtonetrinnene, målt i Hz. For å gå opp et halvtonetrinn, kan vi ikke legge til en fast frekvens. Vi må istedet multiplisere frekvensen med en faktor. Når vi har 12 halvtonetrinn i en oktav er denne faktoren 12-roten av 2, eller 1.05946. Musikalske skalaer vil bli omtalt senere.
Vi har sett at både amplityde og frekvens oppfattes logaritmisk av øret. Det viser seg at de fleste sanser virker på samme måte: Multipliserer vi et stimulus med en faktor, oppfattes dette som et fast tillegg. Dette gjelder vår oppfattelse av lys, varme, smak, lukt, tid osv. At sammenhengen mellom stimuli og persepsjon er logaritmisk, (Fechners lov) ble først påstått av G. T. Fechner i boka Elements of Psychophysics i 1860.
Hvis kurveformen ikke er periodisk, kan dette bety to ting. Enten er kurven en sum av to eller flere periodiske kurver med frekvenser som ikke står i enkle forhold til hverandre. Kurven kalles da kvasiperiodisk, og vil oppfattes som en dissonant akkord. Dette vil bli omtalt senere. Den andre muligheten er at kurven er "bare rot", og ikke er en enkel sum av et lite antall periodiske kurver. Dette vil oppfattes som en susing eller støylyd, ofte uten noen bestemt tonehøyde (unpitched).
Den tredje parameteren, klangfargen, er en svært kompleks ting, og bestemmes av lydkurvens form.
Figur 3.2 viser fire ulike periodiske og statiske lyder. De har samme frekvens og amplityde, og vil alle oppfattes som kontinuerlige toner med samme tonehøyde og omtrent samme lydstyrke. Men kurvene har ulik form. Vi ser en sinustone, en sagtanntone, en firkanttone og et pulstog. Dette gir ulik klangfarge for de forskjellige lydene.

Figure 3.2: Forskjellige kurveformer
Matematikeren Fourier viste at enhver repeterende kurveform kan genereres ved å addere (mikse) et antall sinusoide deltoner, hver med en frekvens som er et heltallsmultiplum av grunnfrekvensen. Figur 3.3 viser prinsippet. Her adderes en sinusformet grunntone med frekvens 100 Hz til en overtone med frekvensen 300 Hz, dvs. en oktav og en kvint over. Resultatet vises i figur 3.4.
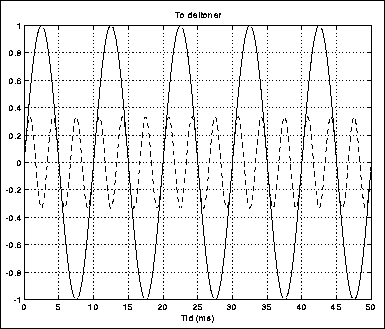
Figure 3.3: Grunntone og andre overtone
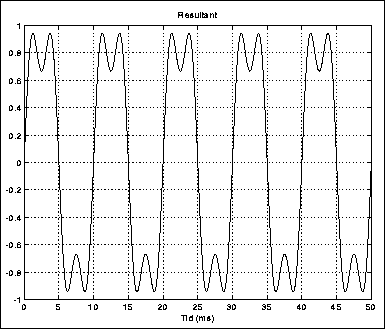
Figure 3.4: Grunntone og andre overtone mikset sammen
De forskjellige deltonene i en ren tone kalles ofte de harmoniske. Grunntonen heter da den første harmoniske, første overtone på to ganger grunnfrekvensen heter andre harmoniske, andre overtone på tre ganger grunnfrekvensen heter tredje harmoniske etc. Som man ser er terminologien litt forvirrende.
I figur 3.3 begynte begge deltonene på samme sted i sinuskurven, dvs. at deltonene har samme fase. Hvis deltonene har ulike faser, vil den resulterende kurveformen naturligvis se annerledes ut. Men øret oppfatter i utgangspunktet ikke faseinformasjon, det oppfatter bare amplityden til de forskjellige deltonene. Forholdet mellom disse amplitydene bestemmer klangfargen. Vi kan med andre ord ha to lyder som ser radikalt ulike ut på et oscilloskop, fordi de har ulik faseinformasjon, men som låter nøyaktig likt, fordi deltonenes amplityder er de samme.
Dersom vi er interessert i klangfarge, er det derfor mest praktisk å beskrive lyden i et stolpediagram der deltonenes amplityder er vist som funksjon av frekvensen. En slik figur kalles et spektrogram, og kan avbildes ved hjelp av et måleinstrument som kalles en spektralanalysator eller spektrograf. Et spektrogram kan f.eks. se ut som i figur 3.5. Overtonene er gjerne svakere enn grunntonen. Legg også merke til de to "toppene" rundt den 9. og den 15. harmoniske. Slike topper er typiske i naturlig lyd, og kalles resonanser (fonetikerne bruker begrepet formanter).
Dette er altså en enkel tone med en veldefinert tonehøyde. Kurveformen er da som vi har sett periodisk, og spektrogrammet består av adskilte stolper med fast avstand lik grunntonens frekvens. Vi sier at spekteret er diskret.
Hvis lyden ikke er periodisk, og dermed uten tonehøyde, vil vi kunne få et kontinuerlig spektrum der alle mulige frekvenser er tilstede. Dette er typisk for støylyder. Spektrogrammet kan da se ut f.eks. som i figur 3.6 (oftest er det langt mer "hårete").
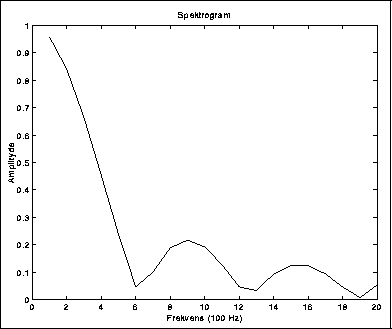
Figure 3.6: Kontinuerlig spektrum
Dersom en lyd vises som et oscillogram, sier vi at lyden er representert
i tidsdomenet. En lyd vist som et spektrogram er representert i
frekvensdomenet. Det er viktig å forstå at disse to
representasjonsformene inneholder den samme informasjonen, dersom vi
ser bort fra faseforhold.
![]() Omregningen mellom tidsdomenet og frekvensdomenet foretas ved hjelp av
en spesiell regnemetode som kalles Fouriertransformasjon.
Fouriertransformasjon er sentral i digital lydbehandling. Omregningen
fra tidsdomenet til frekvensdomenet kan vi også kalle
spektralanalyse. Omregningen fra frekvensdomenet til tidsdomenet
kan vi kalle additiv syntese, fordi vi adderer sammen alle de
sinusoide deltonene i spekteret for å lage en lyd i tidsdomenet.
Omregningen mellom tidsdomenet og frekvensdomenet foretas ved hjelp av
en spesiell regnemetode som kalles Fouriertransformasjon.
Fouriertransformasjon er sentral i digital lydbehandling. Omregningen
fra tidsdomenet til frekvensdomenet kan vi også kalle
spektralanalyse. Omregningen fra frekvensdomenet til tidsdomenet
kan vi kalle additiv syntese, fordi vi adderer sammen alle de
sinusoide deltonene i spekteret for å lage en lyd i tidsdomenet.
Hittil har vi betraktet lyd som ikke endrer seg over tid. Dette gir kontinuerlige toner. Skal vi lage musikk, må selvsagt de tre parametrene i lyden forandre seg hele tiden.
Dynamikk i amplityden
Dynamikk i amplityden er det første vi må få til. Alle musikkinstrumenter fungerer slik at amplityden forandrer seg i løpet av hver tone. En note på en gitar f.eks. starter med en svært hurtig øking av amplityden (attack) fulgt av en langsom utdøing (decay). Dette kan vises i en graf som figur 3.7.
En slik graf kalles en envelope.
![]() Når vi skal syntetisere lyd er det selvsagt ønskelig å kunne
tegne enhver envelope, og dette er mulig med datamaskiner. Mange synthesizere
begrenser seg imidlertid til en generalisert envelope-type med fire
linjesegmenter. Dette heter ADSR, for Attack-Decay-Sustain-Release
(figur 3.8).
Knekkpunktene mellom segmentene kan plasseres fritt av brukeren. Bemerk at
linjene ikke er rette, dette kommer av den ulineære sammenhengen mellom
amplityde og oppfattet lydstyrke. Attack-biten er litt rar, og gir ikke
et naturlig crescendo. Det viser seg imidlertid at naturlige instrumenter
ofte oppfører seg på en liknende måte.
Når vi skal syntetisere lyd er det selvsagt ønskelig å kunne
tegne enhver envelope, og dette er mulig med datamaskiner. Mange synthesizere
begrenser seg imidlertid til en generalisert envelope-type med fire
linjesegmenter. Dette heter ADSR, for Attack-Decay-Sustain-Release
(figur 3.8).
Knekkpunktene mellom segmentene kan plasseres fritt av brukeren. Bemerk at
linjene ikke er rette, dette kommer av den ulineære sammenhengen mellom
amplityde og oppfattet lydstyrke. Attack-biten er litt rar, og gir ikke
et naturlig crescendo. Det viser seg imidlertid at naturlige instrumenter
ofte oppfører seg på en liknende måte.
Vi kan også la amplityden kontrolleres delvis av en lavfrekvent sinusoid. Dette lager en effekt som heter tremolo.
Dynamikk i frekvens
Dynamikk i frekvens er selvsagt nødvendig for å få fram forskjellige noter, men det er også vanlig å variere frekvensen kontinuerlig, enten fra en note til en annen (glissando), eller ved hjelp av en lavfrekvent sinusoid (vibrato).
Dynamikk i klangfargen
For at lyden ikke skal bli helt død, må klangen endres hele tiden. Denne kompliserte oppgaven forsøkes løst på ulike måter ved hjelp av forskjellige syntesemetoder.
Spektrogrammene vi har sett på viser klangen bare på ett bestemt tidspunkt. Når klangen varierer over tid, må vi bruke diagrammer som forsøker å vise lyden i tre dimensjoner (vi får en tidsakse i tillegg til frekvens- og amplitydeaksene). Dette kan gjøres i et "landskapsdiagram" der frekvensen går mot høyre og tiden går innover i bildet (figur 3.9).
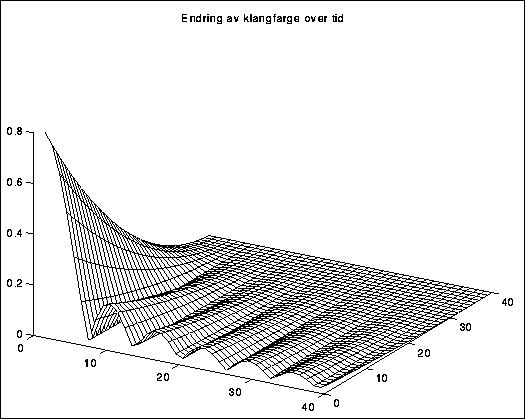
Figure 3.9: Tredimensjonalt spektrogram
Slike diagrammer kan være vanskelige å lese. En representasjonsform som ofte er mer praktisk er sonogrammet, der tiden løper langs x-aksen, frekvensen langs y-aksen og amplityden vises som gråtoner (figur 3.10).