Trigonometri betyr trekantmåling. Når vi studerer forholdene mellom sidene i rettvinklede trekanter (trekanter hvor ett hjørne er rettvinklet), dukker det opp såkalte trigonometriske funksjoner: Sinus, cosinus, tangens etc. Disse funksjonene er morsomme i seg selv, men det underlige er at de samme funksjonene dukker opp overalt i fysikken. Trigonometriske funksjoner brukes til å beskrive f.eks. en pendels bevegelser og bølger på havet. Trigonometriske funksjoner er sentrale også i forbindelse med akustikk og vibrasjon i musikkinstrumenter, og er derfor av spesiell interesse for oss. Summetonen i telefonen er en temmelig ren sinusfunksjon.
En rettvinklet trekant består av de to sidene som ligger inntil
den rette vinkelen (de to katetene) og den siste, "skrå" siden
(hypotenusen). Vi kaller lengden til katetene for a og b, og
lengden til hypotenusen for c. En av vinklene kaller vi 
.
Det der var en gresk bokstav som heter phi. Den ser flott ut på
papiret, og er "standardbokstaven" for vinkler.
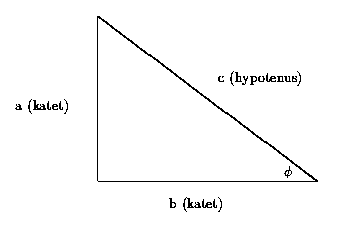
Figure 2.8: Rettvinklet trekant
Forholdene mellom a, b og c er gitt ved Pythagoras' teorem:
som vi uttaler "kvadratet på hypotenusen er summen av kvadratene på katetene".
Eksempel 5: Avstanden til en lydkilde
Anta at en lytter er plassert i origo i et koordinatsystem, altså i punktet (0,0). Vi ønsker å simulere at en lydkilde beveger seg i planet på en eller annen måte, og vi har allerede beregnet (x,y)-koordinatene til lydkilden.
Som en del av simuleringen må vi kontrollere tidforsinkelsen fra lyden sendes ut til den mottas av lytteren. Dette vil gi en fin Doppler-effekt når lydkilden beveger seg. Denne tidsforsinkelsen avhenger direkte av avstanden til lydkilden. Vi må også kunne kontrollere amplityden, som faller som en direkte hyperbelfunksjon av avstanden (lydstyrken vil da falle med kvadratet av avstanden).
Alt dette koker dermed ned til at vi må finne avstanden s fra punktet (0,0) til punktet (x,y). Ved å tegne opp situasjonen i et koordinatsystem, ser vi at vi får en rettvinklet trekant, og fra Pythagoras har vi
Du er sikkert vant til at vinkler måles i grader. Når vi arbeider med matematikk og datamaskiner måler vi derimot nesten alltid vinkler i radianer.
180 grader tilsvarer 
radianer, slik at 1 radian er 180/ ,
ca 57 grader (husk at 
).
Eksempelvis er da 30 grader 
radianer, 45 grader 
radianer, 90 grader 
radianer. Vi kutter som oftest ut enheten
radianer, og sier f.eks. at vinkelen 
.
La oss gå tilbake til tegningen av den rettvinklede trekanten.
Vi definerer nå en funksjon 
på denne
måten:
som vi uttaler "sinus til en vinkel er forholdet mellom den motstående
katet og hypotenusen". Ettersom varierer, må lengdene til sidene
variere for at vi fortsatt skal ha en rettvinklet trekant. Forholdet mellom
motstående katet og hypotenusen vil alltid følge den samme funksjonen
, uansett hvor stor trekanten er.
I trekanten over gir det ikke mening å snakke om større
enn . Vi utvider derfor definisjonsområdet til å omfatte
alle mulige tall, positive og negative, og definerer hvordan 
skal
variere her (geometrisk gjøres dette ved å studere den såkalte
enhetssirkelen, men det hopper vi over nå).
Sinusfunksjonen er vist i figur 2.9.
Det viktigste å legge merke til her er at sinusfunksjonen er
periodisk, med periode 
. Dette betyr at funksjonen
gjentar seg bortover i det uendelige. Hvis vi fester en blyant på
en svingende pendel, og lar blyanten tegne på et langt papir som
vi trekker forbi pendelen, så vil vi få en graf som denne.
En pendel beskrives altså ved en sinusfunksjon, og i naturen er
det svært mange prosesser som oppfører seg som pendler.
Vi kan styre frekvensen, dvs. hvor mange ganger sinuskurven gjentar seg hvert sekund, ved å lage oss funksjoner av typen
der f er frekvensen i svingninger pr. sekund og t er tiden i sekunder. Enheten "svingninger pr. sekund" har fått et eget navn, Hertz, forkortet Hz. Hvis frekvensen f.eks. er 5 Hz, ser funksjonen ut som vist i figur 2.10.
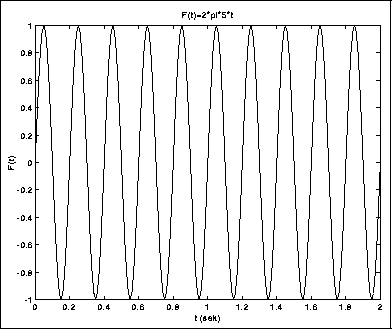
Figure 2.10: Sinusoid funksjon
Tilbake til den rettvinklede trekanten igjen.
Vi definerer nå en ny funksjon 
på denne
måten:
som vi uttaler "cosinus til en vinkel er forholdet mellom den hosliggende katet og hypotenusen".
Vi utvider igjen definisjonsområdet, og får funksjonen vist i figur 2.11.
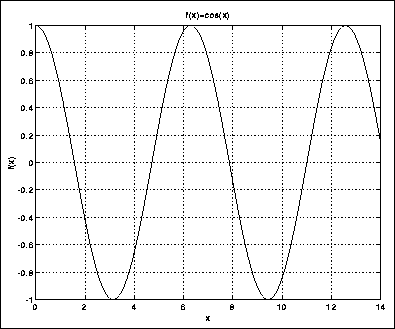
Figure 2.11: Cosinusfunksjonen
Denne grafen er identisk med grafen for sinus, bortsett fra at den er forskjøvet et stykke i horisontal retning. Vi sier at sinus og cosinus, uansett frekvens, begge er sinusoider, men at de har forskjellig fase. Hvis vi spiller en sinusoid ut gjennom en høyttaler, vil vi høre en ren, myk tone. Tonehøyden vil avhenge av frekvensen, men fasen vil ikke ha noen betydning for hvordan lyden oppfattes.
Det må bemerkes at man ofte bruker ordet "sinus" om alle sinusoider, uavhengig av frekvens og fase. Dette er ikke helt korrekt, fordi sinus er en strengt definert funksjon med en bestemt periode og fase.
Vi har nå definert sinus og cosinus, og vi har sett at begge er bølgeformede, periodiske funksjoner.
Enhver periodisk funksjon kan konstrueres ved å summere et antall sinus- og cosinus-funksjoner, hver med en frekvens som er et heltallsmultiplum av frekvensen til den periodiske funksjonen.
Dette er Fourier's teorem, og en sum av sinuser og cosinuser som bygger opp en funksjon heter en Fourier-rekke. Fourier's teorem er et av de dypeste og vakreste resultater i matematikken.
Dette er veldig viktig når vi driver med lyd, for øret oppfatter som hovedregel en lyd i frekvensdomenet, dvs. som de sinusoidene som den er bygget opp av. Dette er nærmere forklart i heftet om akustikk.
Bemerk at vi enten kan spesifisere en Fourier-rekke som en sum av ekte sinus- og cosinus-funksjoner, eller som en sum av sinusoider der fasen er oppgitt. Dette er likegyldige betraktningsmåter, fordi vi kan lage en sinusoid med hvilken som helst fase ved å addere en sinus og en cosinus med de riktige amplityder.
Dersom funksjonen vi ønsker å konstruere har sprang (diskontinuiteter), må vi i prinsippet addere et uendelig antall sinusoider. Dette er imidlertid ikke av interesse for oss. Alle digitale lyder er nemlig båndbegrensede, og inneholder bare frekvenser opp til halve samplingfrekvensen.
Fourier's teorem omhandler periodiske funksjoner. Men hva så med ikke-periodiske funksjoner? De kan også håndteres, på en av to måter. Enten sier vi at en funksjon bare er definert i et avgrenset område (en lyd varer f.eks. bare en viss tid). Vi utvider så funksjonen periodisk, dvs. at vi later som om funksjonen gjentar seg periodisk utenfor det opprinnelige definisjonsområdet. Funksjonen er så klar for Fourier's teorem, og vi kan etterpå glemme funksjonsverdiene utenfor det opprinnelige området.
Den andre angrepsmåten er å si at funksjonen faktisk er periodisk, men med uendelig lang periode. Grunnfrekvensen blir da uendelig liten, og de øvrige sinusoidene kommer uendelig nær hverandre. Fourier-rekka går da over til et Fourier-integral.
Disse tingene blir forhåpentlig mer intuitivt forståelige når vi ser på anvendelsene innen akustikken.
