Funksjoner

Den viktigste ideen i matematikken må vel være funksjonsbegrepet. Vi skal se litt på dette, og dessuten presentere en zoo av funksjoner som man trenger i sin verktøykasse når man skal konstruere musikalske forløp.

Hva er en funksjon?

En funksjon er en regel som anvendes på et tall x som vi putter inn i funksjonen, og som leverer et annet tall f(x). Selve regelen kalles funksjonsforskriften.

Eksempler:

vil levere tallet 1 uansett hvilken x man putter inn (dette kalles en konstant funksjon).

vil sende ut samme tallet som vi sendte inn (dette kalles identitetsfunksjonen).

vil addere 1 til tallet vi sendte inn (dette er en lineær funksjon, se under).

Vi kan betrakte en funksjon som en maskin som omformer tall. Når vi arbeider med musikkprogrammet MAX, vil en funksjon i praksis bety en liten boks på skjermen med en inngang og en utgang, hvor vi har skrevet funksjonsforskriften inne i boksen.

Vi skal se på endel spesielle funksjoner under, men først må man ha klart for seg hva en funksjonsgraf er. En slik graf er en framstilling av funksjonsverdiene plassert i et koordinatsystem. Vi plotter alle ``fornuftige'' x (de som tilhører funksjonens definisjonsområde) og deres tilhørende funksjonsverdier f(x), slik man er kjent med fra alle mulige kurver i avisene. En kurve fra børsen framstiller tiden langs x-aksen, og aksjekursen til ethvert tidspunkt som f(x)-verdier.

Med blant funksjonene hører også funksjoner av flere variable, f.eks.

og funksjoner som opererer på andre typer objekter enn vanlige tall (vektorer, matriser, komplekse tall).

Lineære funksjoner

En lineær funksjon er på formen

der a og b er faste tall som vi velger. Eksempel:

Her er a=2 og b=3. Det betyr at funksjonen multipliserer x med 2 og legger til 3.

Det finnes endel spesialtilfeller av lineære funksjoner, f.eks. nullfunksjonen f(x)=0 der a=0 og b=0, identitetsfunksjonen f(x)=x der a=1 og b=0, konstante funksjoner f(x)=b og multiplikasjon med konstant f(x)=ax.

Lineære funksjoner har fått sitt navn fordi deres graf alltid er en rett linje, som vist i figur 2.1.

 
Figure 2.1:  Lineær funksjon

Legg merke til at konstanten a (her 2) styrer hvor bratt kurven er, mens konstanten b (her 3) bestemmer verdien f(0).

Lineære funksjoner er på mange måter spesielle, og lette å håndtere. For eksempel er det bare lineære funksjoner og forsinkelsesfunksjoner (se under) som slipper igjennom lyd uten at klangfargen endres.

Polynomer

Dersom vi multipliserer et tall x med seg selv ( ) sier vi at vi har opphøyet tallet i andre potens, og vi skriver .

Eksempel: .

Grafen til er en såkalt parabel, og er vist i figur 2.2.

 
Figure 2.2:  Parabel

Her er det at par ting å legge merke til. For det første ser vi at alle negative x-verdier ender opp som positive f(x). For det andre er det tydelig at grafen er symmetrisk om x=0; formelt skriver vi f(x)=f(-x) (kan du finne ut av det?). Vi sier også at er en like funksjon.

Figur 2.3 viser grafen til .

 
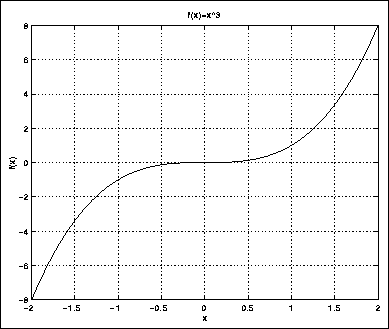
Figure 2.3:  Tredjegradspolynom

er antisymmetrisk, slik at f(x)=-f(-x). Vi sier også at er en odde funksjon. Det gjelder generelt at like tall i potensen gir like funksjoner, og odde tall i potensen odde funksjoner.

Vi skal nå se på funksjoner som er en sum av de typer funksjoner vi har behandlet hittil. For eksempel er en sum av funksjonen (riktignok med en faktor 3 foran), og den lineære funksjonen 2x+1. En slik funksjon kalles et polynom. Polynomer har en grad etter den høyeste potensen som inngår.

Eksempler:
5x+2 og 3x er polynomer av 1. grad.
er et polynom av 2. grad.
er et polynom av 14. grad.

Det finnes mange forskjellige spesielle klasser av polynomer, hvor koeffisientene er konstruert etter bestemte regler. F.eks. er det de såkalte Bessel-polynomene som bestemmer styrken på deltonene i spektret ved FM-syntese.

Eksempel 1: Simulering av rørforsterker

En forsterker tar et inngangssignal x og forsterker det med en faktor a, som styres av en volumkontroll. En forsterker kan dermed beskrives ved en såkalt overføringsfunksjon. Ideelt sett er forsterkeren lineær, det vil si at den har en lineær overføringsfunksjon f(x)=ax. La oss anta at a=3 (det spiller ingen rolle), slik at en ideell forsterker har f(x)=3x som overføringsfunksjon. Lyden går da gjennom forsterkeren uten å endres i det hele tatt, bortsett fra at amplityden tredobles.

Alle virkelige forsterkere har imidlertid en større eller mindre grad av forvrengning, slik at f(x) avviker fra en lineær funksjon. En typisk effekt er klipping, det vil si at når inngangssignalet får for stor amplityde går forsterkeren i metning og nekter å slippe igjennom mer lyd.

Transistorforsterkere klipper hardt, det vil si at signalet er noenlunde intakt opp til et visst nivå, men så kuttes det brått. Den stygge, sprakende forvrengningen er velkjent for de fleste.

Forsterkere med radiorør klipper derimot mere bløtt, det vil si at det er en gradvis overgang fra ikke-klipping til klipping. Dette lager en spesiell sound som særlig gitarister er glade i. Det finnes til og med egne effektbokser som etterlikner slik ``tube amp sound''. Vi skal lage en slik boks på en datamaskin, og da må vi lage oss en overføringsfunksjon som maskinen kan sende lyden igjennom for å oppnå den riktige effekten. Den norske komponisten Anders Vinjar har holdt på med nettopp dette.

La oss forsøke med et polynom. I utgangspunktet ønsker vi at forsterkeren skal være lineær, så vi setter f(x)=3x (figur 2.4).

 
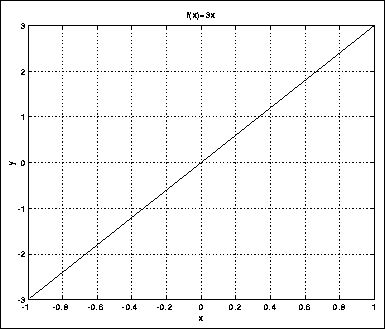
Figure 2.4:  Overføringsfunksjon for lineær forsterker

Det ser jo fornuftig ut, men så må vi prøve å introdusere litt ``soft clipping''. Dette innebærer at grafen må flate ut gradvis i endene. På den måten vil store x (nær pluss og minus 1) bli begrenset.

Vi kan forsøke å trekke fra en , så vi får overføringsfunksjonen . Det er ikke så dumt, for som vi ser av grafen for over ligger den nær null når x er nær null, slik at vår lineæritet ikke ødelegges for små x. For større x blir imidlertid utslagene store, og de vil slå riktig vei dersom vi trekker fra 3x (figur 2.5).

 
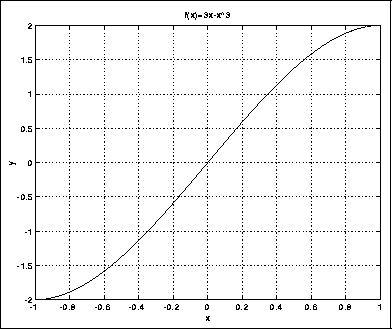
Figure 2.5:  Overføringsfunksjon for ulineær forsterker

Dette tredjegradspolynomet kan vi sette inn i en MAX-patch eller i et C-Sound-program og oppnå en utmerket ``tube amp''. Vi har nå sett et eksempel på en lydbehandlingsmetode som kalles ulineær kurveforming eller nonlinear waveshaping. I ulineær kurveforming benyttes ofte en spesiell type polynomer som heter Chebychev-polynomer. Chebychev-polynomer har pene egenskaper som gjør det lett å forutsi hvordan klangfargen endres.

Hyperbler og røtter

Funksjonen kalles en hyperbel. Her må vi huske på at definisjonsområdet ikke inneholder null, fordi divisjon med null er forbudt.

De motsatte funksjonene av potensene over kalles røtter. Det tallet som opphøyet i andre potens gir x, heter kvadratroten til x, og vi skriver . Kvadratroten til 9 er således 3, kvadratroten til 16 er 4. Igjen må vi passe på definisjonsområdet. Det er forbudt å ta kvadratroten av et negativt tall, for det finnes ingen tall som opphøyet i andre potens gir et tall mindre enn null.

Det tallet som opphøyet i tredje potens gir x, heter kubikkroten eller tredje-roten av x, og vi skriver . Her er det tillatt å putte inn negative x (finn ut hvorfor!).

Tilsvarende kan vi definere høyere røtter. De fleste programmeringsspråk har imidlertid ikke egne funksjoner for annet enn kvadratrøtter. Det er lett å lure fram høyere røtter ved å benytte seg av måten ikke-heltallige potenser er definert på. Vi har for en n'te rot at

slik at f.eks. fjerderoten av x kan skrives som .

Eksponensialfunksjoner, logaritmer

Hvis vi bruker potenser som beskrevet over, men setter x i eksponenten i stedet for i grunntallet, får vi en eksponensialfunksjon. Dette er en meget nyttig funksjon og er blant de mest brukte til musikkformål.

Eksempler på slike funksjoner er , , . I disse eksemplene brukte vi 2, 3 og 3.14 som grunntall (det tallet vi opphøyer i noe). Siden vi alltids kan skru til disse funksjonene som vi vil ved å multiplisere med faktorer etc., er det på en måte likegyldig hvilket grunntall vi bruker. I matematikken viser det seg at alle formler blir mye enklere dersom vi alltid bruker et magisk tall som heter e som grunntall. Vi skal ikke gå mer inn på årsakene til dette, men vi bør være klar over det, bl.a. fordi datamaskiner oftest har en funksjon som vi kan benytte oss av. Tallet e er forøvrig omtrent 2.71, og er like viktig som for matematikerne.

Funksjonen stiger mer og mer, og brattere og brattere. Før eller senere, for store nok x, blir den faktisk større enn alle tenkelige polynomer. Grafen er vist i figur 2.6 (legg merke til at ):

 
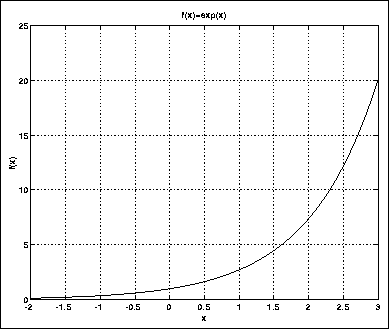
Figure 2.6:  Eksponensialfunksjonen

Noen regneregler for funksjoner med potenser kan være nyttige:

De omvendte funksjoner av eksponensialfunksjoner heter logaritmer. Det finnes forskjellige typer logaritmer, avhengig av hvilket grunntall vi snakker om. Logaritmen til x, med grunntall 10, skriver vi , og vi mener da at f(x) er det tallet vi må opphøye 10 i for å få x (det der krever kanskje litt fordøying). Vi har dermed f.eks. at og .

Logaritmen med grunntall e kalles den naturlige logaritmen, og skrives . Vi har dermed at . Den logaritmefunksjonen som oftest finnes på datamaskiner, og som gjerne heter log, er den naturlige logaritmen.

En viktig regneregel for logaritmer er at . Siden er den motsatte (inverse) funksjonen av , har vi også at ; hvis vi tar e og opphøyer i den naturlige logaritmen til x, får vi simpelthen x tilbake. Disse to regnereglene kan vi bruke til å lage oss potenser dersom programmeringsspråket vårt ikke har dette tilgjengelig (dette er faktisk svært vanlig):

Eksempel 2: Beregning av frekvens fra notenummer

Et av de vanligste spørsmålene som dukker opp i denne bransjen er følgende: Vi har et MIDI notenummer (60 for C, 61 for Ciss etc.). Hvilken frekvens i Hz tilsvarer dette?

Vi skal ikke gå igjennom teorien om skalaer her, men anta at vi vil bruke ``equal temperment''. Vi går ut fra at kammertonen A har frekvensen 440 Hz. Nå er det slik at vi vil få neste halvtone ved å multiplisere frekvensen med en konstant k. Når vi har multiplisert 12 ganger skal vi ha gått opp en oktav, dvs. at frekvensen skal være doblet. For å oppnå dette setter vi . Hvis MIDI-noten til kammertonen er 69, får vi frekvensen

for MIDI-note n. Dette er en eksponensialfunksjon, og dette viser at øret ikke oppfatter frekvens lineært. Bemerk også at n ikke behøver å være et helt tall, så mikrotonalitet håndteres problemfritt med denne formelen.

En datamaskin vil kanskje ha formelen på denne måten:

f=440*pow(1.0594631,(n-69));

eller i verste fall slik:

f=440*exp((n-69)*log(1.0594631));

Eksempel 3: Beregning av notenummer fra frekvens

Det å finne et MIDI-notenummer fra en frekvens i Hz er også ofte nyttig. Da tar vi simpelthen formelen fra forrige eksempel og løser likningen med hensyn på n. Dette gjøres ved å ta den naturlige logaritmen på hver side av likhetstegnet, og deretter anvende regnereglene som er gitt over:

Dette er en logaritme-funksjon. På en datamaskin skriver man noe slikt:

n=(log(f)-log(440))/log(1.0594631)+69;

Eksempel 4: Eksponensielle kontrollfunksjoner

Som vi har sett, så er eksponensialfunksjoner fornuftige å bruke dersom vi vil at øret skal oppfatte en jevnt glidende tonehøyde. Amplityder bør også styres med slike funksjoner, fordi øret oppfatter lydstyrke på en liknende måte. Eksponensialfunksjoner er dermed mye brukt i omhyllingskurver (envelopes) og andre kontrollfunksjoner. Spesielt velkjent er envelopes av ADSR-typen (Attack-Decay-Sustain-Release). Slike envelopes består av tre eksponensialfunksjoner som er satt sammen, samt en konstant Sustain-fase.

I C-Sound og mange andre systemer finnes en funksjonsgenerator som lar brukeren spesifisere start- og endepunkter for slike eksponensialfunksjoner. Hvis vi programmerer f.eks. i C, kan vi bruke noe slikt:

Hvis vi lar x løpe fra 0 til 1, vil f(x) løpe fra startverdi til sluttverdi, med en eksponensiell form som bestemmes av a (positiv eller negativ). Figur 2.7 viser noen eksempler.

 
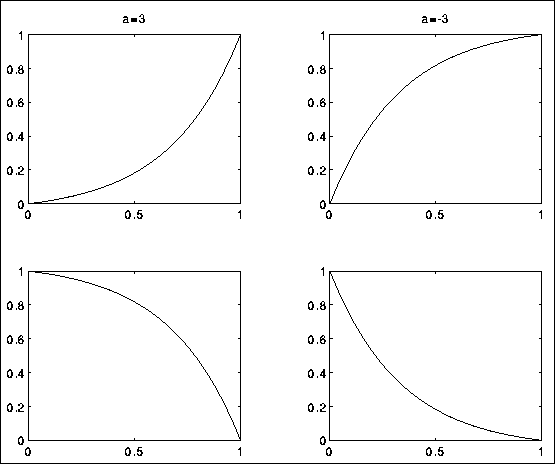
Figure 2.7:  Eksponensielle kontrollfunksjoner