I dette kapittelet skal vi se på en måte å betrakte lyd på
som kan virke uvant etter alt snakket om kontinuerlige sinusoider og
varierende spektre. Det går an å se på lyd som et aggregat av
utallige små "korn" (grains) som er plassert rundt i frekvens og/eller
tid. Vi kan syntetisere lyd ved å pøse på med slike korn, vi
kan forsøke å finne ut hvilke korn av en valgt type vi må
benytte for å bygge opp en lyd vi analyserer, eller vi kan klippe opp
en lyd i små biter som vi behandler på ulike måter. Alt dette
kan vi kalle granulære lydbehandlingsmetoder, etter det latinske
ordet granula (korn).
Hva slags korn vi vil benytte i f.eks. granulær syntese er igrunnen
valgfritt. Akustisk vil det gjerne dreie seg om små "plopp" av type
dryppende vannkran eller vibrafon. Disse ploppene kan f.eks. spres ved hjelp
av tilfeldighetsgeneratorer i "skyer". Å bygge opp en lyd med slike korn
har en parallell i pointilismen. Dette var en retning innen
impresjonismen der man malte bilder ved å avsette tusener av små
fargepunkter på lerretet.
VOSIM-syntese (for VOice SIMulation) er en granulær syntesemetode som opprinnelig ble laget for talesyntese. Kornene har her en spesiell form med parametre som vi kan velge. Hvert korn består av et lite pulstog med N klokkeformede pulser (kvadrert sinus er fint), hver med en pulsbredde w. Etter den første pulsen multipliseres påfølgende pulser med en dempningsfaktor d;SPMlt;1. Hele pulstoget gis en amplityde a, og så gjentas kornene med en periode L som bestemmer grunntonefrekvensen (f=1/L).
Figur 5.29 viser en bit av et VOSIM-signal, med to korn.
Ved hjelp av parametrene kan vi styre pitch, amplityde og klangfarge. En enkelt VOSIM-generator lager et spektrum med en enkelt formant. For flere formanter, bruker vi flere VOSIM-generatorer.
VOSIM ble utviklet ved Institutt for Sonologi i Utrecht, Nederland. Metoden har ikke noen stor utbredelse i dag.
En FOF (Forme Onde Formantique), er et lite korn som består av en sinus med en eksponensiell envelope. På samme måte som i VOSIM, vil syntese med en enkelt FOF-generator gi et spektrum med en enkelt formant. Miksing av flere ulike FOF-generatorer gir et spektrum med flere formanter, som kan brukes til syntese av f.eks. tale og sang.
En FOF kan tolkes som en enkelt impuls fra stemmebåndene, som er
filtrert av hals og munnhule. Hvis man trekker pusten inn, kan man klare
å lage enkeltstående FOF'er som kan høres separat
.
En slik liten kurveform, som er filterets
respons på en impuls, kalles naturlig nok filterets impulsrespons.
Et filter er fullstendig karakterisert ved sin impulsrespons; ja faktisk
er frekvenskarakteristikken ikke noe annet enn Fouriertransformasjonen
til impulsresponsen. Ved invers Fourier-transformasjon kan vi dermed
gå fra frekvensrespons til impulsrespons. Hvis vi sampler denne
impulsresponsen, kan vi benytte samplene direkte som filterkoeffisienter
i et ikke-rekursivt filter. (Dette avsnittet var en digresjon, men det
ville være synd om ordet "impulsrespons" ikke ble nevnt i en
tekst om digital lydbehandling).
Programmet Chant fra IRCAM benytter FOF-syntese. Det finnes en meget imponerende syntese av "Nattens Dronning" av Mozart som er laget med dette systemet. C-Sound inneholder også en FOF-generator.
I forbindelse med granulær syntese må vi også nevne amerikaneren Barry Truax og svensken Peter Lundén, som begge har laget stykker som illustrerer metoden godt. "Riverrun" av Truax anbefales spesielt.
Vi kan "granulere" en lyd ved å klippe den opp i små biter med en varighet på typisk mellom 20 og 500 millisekunder. Disse bitene kan så komprimeres eller strekkes, forsterkes eller dempes, filtreres etc. uavhengig av hverandre, eller de kan omkastes (permuteres) på forskjellige måter. Det er ikke lurt å klippe av lydkornene brått. Hvis vi f.eks. bytter om rekkefølgen kan vi da risikere at kurven gjør sprang i overgangen mellom kornene. Slike diskontinuiteter gir klikk. Vi legger derfor på envelopes på hvert lille korn, som faller pent ned mot null i hver ende. Det benyttes samme type vindusfunksjoner som vi så på under diskusjonen om FFT (Hanning etc.). Det er vanlig å la vinduene overlappe.
Ved å strekke og komprimere kornene kan vi gjøre pitch-skift og time-stretch med relativt lav kvalitet. Nesten alle kommersielle harmonizere benytter granulering med vindusfunksjoner. Det begynner nå å komme effektbokser som utfører morsomme granuleringsmetoder med tilfeldighet etc. IRCAM-arbeidsstasjonen er også velegnet til granulering, og dette har vært brukt av bl.a. Philippe Manoury og Rolf Wallin.
Hvis vi passer på å klippe opp lyden akkurat på de tidspunktene der kurven passerer null-nivået på vei oppover, kan vi unngå klikk uten å modulere med vindusfunksjoner. Dette medfører at kornene vil variere i lengde: I perioder med høye frekvenser eller støylyder får vi mange nullgjennomganger og små korn, mens i perioder med lave frekvenser, stillhet eller fattig spektrum får vi store korn.
En spesiell effekt får vi ved å avspille disse kornene i et spiralformet mønster på denne måten:
1 2 3 4 5, 3 4 5 6 7, 5 6 7 8 9, 7 8 9 10 11, etc.
Her er inkrementet satt til 2 nullgjennomganger, mens vindus-størrelsen er satt til 5 biter mellom påfølgende nullgjennomganger. Dette vil strekke lyden ut i tid, og gi artige effekter.
Det var den sveitsiske komponisten Rainer Boesch som gjorde oss i Norge oppmerksom på denne typen teknikker, og vi har siden benyttet dette flittig. I stykket "Strøk" av Rolf Wallin er hardingfelemusikk behandlet ved hjelp av granulering med nullgjennomgangsanalyse. Den norske lydbehandlingsmaskinen "Fredag" ble i sin tid konstruert med spesiell hardware og software som kunne (og forsåvidt fortsatt kan) utføre dette i sann tid med endel spesielle fiduser.
Ved korttids-FFT betrakter man små biter av lyden av gangen. Hver av disse bitene blir dekomponert i sine enkelte sinusoide bestanddeler. Analysen gir oss derfor et stort antall små sinusoide biter som er plassert i tid og frekvens. Vi kan dermed betrakte korttids-FFT som en metode som finner ut hvilke sinusoide korn vi må bruke for å bygge opp lyden. Invers FFT kan da betraktes som en granulær syntese som resyntetiserer lyden ut fra informasjonen om alle disse små kornene.
Dette er en litt uvanlig måte å se på korttids-FFT på. Når vi tenker i granulære baner, blir det naturlig å gjøre ting som å plukke vekk korn, permutere korn i tid og frekvens etc. Vi kan også resyntetisere med andre typer korn enn sinusoider, f.eks små plinger generert av Karplus-strong-algoritmen.
NoTAM bedriver utvikling av et lite program for våre SGI-maskiner som retter seg inn mot å betrakte korttids-FFT som en granulær metode. Programmet heter Ceres, etter den romerske korn-gudinnen.
Det går an å forsøke å dekomponere en lyd i andre typer korn enn små sinusoider. En matematiker vil si at vi benytter en annen basis for dekomposisjonen. I signalbehandling og matematikk benyttes betegnelsen wavelets om våre "korn" ("wavelet" er diminutiv av "wave", og betyr altså "liten bølge"). Det finnes flere ulike klasser av wavelets i bruk. Det finnes også forskjellige algoritmer for å dekomponere en funksjon opp i enkelte wavelets, enkelte er basert på en matematisk operasjon som heter korrelasjon.
Wavelets har vært et hett tema i matematikk og signalbehandling i de senere år. Det viser seg at denne betraktningsmåten har mye for seg både teoretisk og i anvendelser. Støyreduksjon ved wavelet- transformasjon er nå en viktig teknikk.
Vi så i avsnittet om FFT at vi kan styre oppløsningen i tid og frekvens ved å justere N. Med wavelets har vi større frihet til å dele opp frekvens-tid-planet. For eksempel kan vi ha god oppløsning i frekvens ved lave frekvenser, mens vi kan minske frekvensoppløsningen oppover i spekteret slik at tidsbestemmelsen blir bedre (se figur 5.30). Det er slik øret virker.
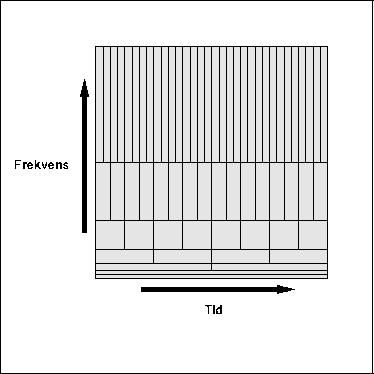
Figure 5.30: Frekvensavhengig oppløsning ved dekomposisjon
i en spesiell type wavelets
Syntese og analyse med generelle wavelets begynner også å få musikalske anvendelser.
