



Next: Granulære metoder
Up: Digital lydbehandling
Previous: Fysisk modellering
Vi har hittil sett mest på lydbehandlingsteknikker som først og fremst
betraktes i tidsdomenet. I dette kapittelet skal vi se på metoder
der vi behandler lydens spektrum, slik at vi beveger oss i frekvensdomenet.
Dette er en noe løs klassifisering, siden enhver operasjon i tidsdomenet
gir en endring i frekvensdomenet og omvendt. Det er, som vi har sett, bare
snakk om to forskjellige måter å representere lydsignalet på.
Et filter er en innretning som endrer et spektrum på en slik
måte at det ikke kommer til nye frekvenskomponenter. For å være
litt mer konkret, kan vi si at et filter generelt demper visse
frekvenser og forsterker andre. Tradisjonelt betraktes følgende
klasser av filterkarakteristikker som særlig viktige:
- Lavpass, der alle frekvenser under en viss frekvens
(cut-off eller klippefrekvens) beholdes, mens høyere
frekvenskomponenter dempes mest mulig (figur 5.17).
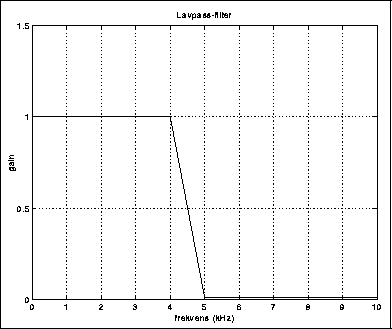
Figure 5.17: Lavpassfilter
Et lavpassfilter kan dermed f.eks. brukes til å dempe støy på
høye frekvenser. Diskant-knappen på stereoanlegget kontrollerer
et lavpassfilter.
- Høypass, der alle frekvenser over klippefrekvensen beholdes,
mens lavere frekvenskomponenter dempes mest mulig (figur 5.18).
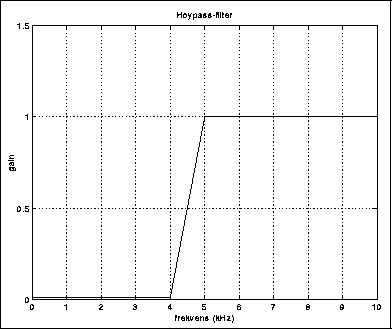
Figure 5.18: Høypassfilter
Bass-knappen på stereoanlegget kontrollerer et høypassfilter.
Et høypassfilter og et lavpassfilter brukes i to-veis høyttalere
for å styre lyd til henholdsvis diskant- og bass-elementet.
- Båndpass, der alle frekvenser innenfor et visst bånd
beholdes, mens frekvenskomponenter utenfor båndet dempes mest
mulig (figur 5.19).
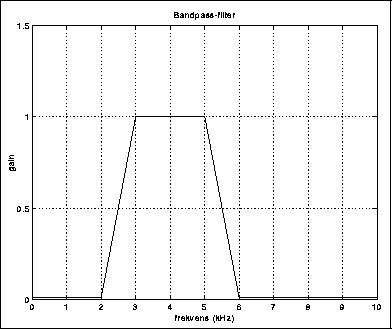
Figure 5.19: Båndpassfilter
Et båndpassfilter kan karakteriseres ved en senterfrekvens (her
4 kHz) og en båndbredde. Ingeniører snakker gjerne om
Q-faktor (godhetsfaktor), som er definert som senterfrekvens delt
på båndbredde. Stor Q betyr dermed liten båndbredde.
Et båndpassfilter med liten båndbredde kan "sveipes" over en
lyd slik at bare en og en deltone slipper igjennom filteret av gangen.
- Båndstopp eller notch, der alle frekvenser utenfor
et visst bånd beholdes, mens frekvenskomponenter innenfor
båndet dempes mest mulig (figur 5.20).
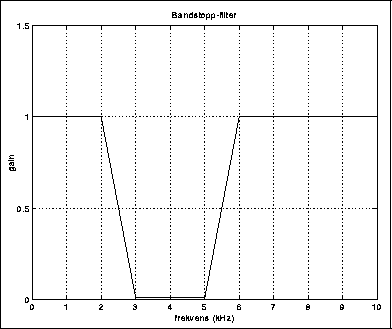
Figure 5.20: Båndstoppfilter
Et båndstoppfilter med liten båndbredde og senterfrekvens 50 Hz
er fint til å fjerne nettbrum med.
- Kamfilter, som vekselvis stanser og stopper frekvensene med
jevne mellomrom oppover i spekteret (figur 5.21).
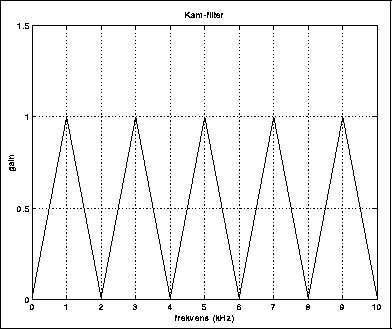
Figure 5.21: Kamfilter
Et kamfilter er fint til å slippe igjennom en grunntone med overtoner,
men dempe alt annet. Vi så en anvendelse for dette i avsnittet om
pitch-følging.
- Allpass, som slipper igjennom alle frekvenser uhindret
(figur 5.22).
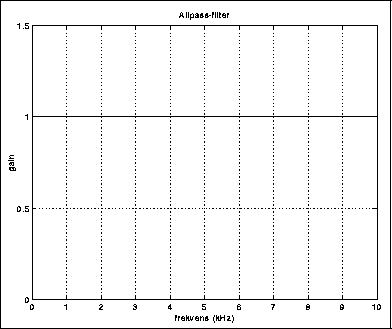
Figure 5.22: Allpassfilter
Hva i all verden er vitsen med det? Et allpassfilter gjør kanskje ingenting
med styrken til de ulike deltonene, men det kan ha stor effekt på
fasen. Dette betyr at man kan konstruere allpassfiltre som slipper
lyden uhindret igjennom, bortsett fra at ulike frekvenser forsinkes ulikt og
derfor kommer ut til forskjellig tid. Dette kalles dispersjon, og
er analogt til spredningen av ulike frekvenser i lys gjennom et prisme.
Det er teoretisk umulig å konstruere et filter hvor flankene er
helt loddrette. Det vil alltid finnes et overgangsområde mellom
passbåndet og stoppbåndet. Generelt må et filter gjøres
mer komplisert jo steilere flanker vi ønsker. De enkleste filtrene
(av første orden) er lavpass- og høypassfiltre som demper
6 dB pr. oktav. Mer kompliserte filtre av annen orden kan dempe 12 dB
pr. oktav. Svære filtre, ofte kalt brick-wall-filtre, kan
dempe kanskje oppimot 100 dB pr. oktav, men da begynner man å få
problemer med bl.a. stor forsinkelse gjennom filteret.
Vi kan lage mer kompliserte karakteristikker og brattere flanker ved å
koble grunntypene over i serie (da vil karakteristikkene multipliseres)
eller parallell (da vil karakteristikkene adderes).
Filtrering kan implementeres meget effektivt på en datamaskin ved hjelp
av differenslikninger. En slik likning angir ett nytt utgangs-sample
som en vektet sum av tidligere inngangs-samples og utgangs-samples. Hvis
x er inngangs-samples og y er utgangs-samples, kan vi skrive
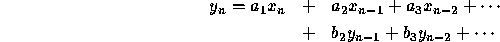
der n er nummeret til "nåværende" sample.
La oss se på et enkelt spesialtilfelle, der vi bare bruker tidligere
inngangs-samples. Vi tar simpelthen gjennomsnittet av de to forrige
inngangs-samplene, og presenterer dette som et nytt utgangs-sample:
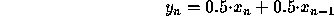
Siden vi tar et løpende gjennomsnitt, vil hurtige variasjoner i
sampleverdiene i en viss utstrekning bli glattet ut. Dette tilsvarer at
høyfrekvente komponenter blir dempet. Det ser dermed ut til at vi
får et slags lavpassfilter. Sender vi således en DC-spenning
gjennom filteret, hvilket tilsvarer en frekvens på 0 Hz, vil denne
passere uendret gjennom filteret. Vekselvis positive og negative verdier
med like stor absoluttverdi, hvilket tilsvarer en komponent på
Nyquist-frekvensen, vil bli dempet fullstendig. Filterkarakteristikken er
vist i figur 5.23 (Nyquist-frekvensen er her 128 Hz).
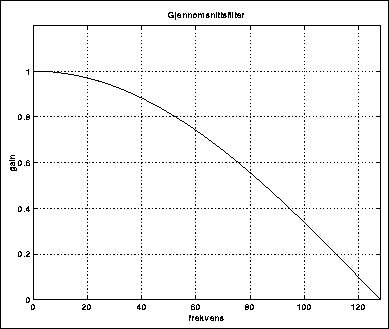
Figure 5.23: Gjennomsnittsfilter
Det kan overlates som en oppgave til leseren å finne ut hvorfor vi
får et høypassfilter hvis vi bytter ut pluss-tegnet i likningen
over med et minus-tegn.
Hvis vi i tillegg tar med tidligere utgangs-samples i differenslikningen,
introduserer vi en feedback i filteret. Vi får da et rekursivt
filter.
Det er en stor vitenskap å bestemme koeffisientene i differenslikningen
slik at vi får en ønsket filterkarakteristikk i frekvensdomenet. Vi
kan ikke gå nærmere inn på dette. I praksis vil man benytte
oppslagsverk og tabeller der man kan finne koeffisienter for forskjellige
slags filtre, der ting som senterfrekvens og båndbredde inngår som
parametre.
Hvis vi har lyden representert i frekvensdomenet, kan vi lage filtre
ved å behandle spekteret direkte. Vi kan gå inn og klippe bort
frekvenskomponenter innenfor visse områder, og forsterke i andre
områder. Det er også mange andre morsomme operasjoner vi kan
utføre i frekvensdomenet.
For å overføre en samplet lyd til frekvensdomenet, må vi
gjøre en frekvensanalyse eller Fourier-transformasjon.
Dette er i utgangspunktet en meget tung regneoperasjon.
Det var derfor en viktig oppdagelse som ble gjort av Cooley og
Tukey på 1960-tallet, da de fant en svært effektiv algoritme for
Fourier-transformasjon. Etterhvert har det kommet flere liknende algoritmer,
som nå går under fellesbetegnelsen Fast Fourier Transform eller
FFT.
FFT er en nokså innfløkt og smart algoritme, men for brukeren er
resultatet greit nok: Man putter en sample-sekvens inn, og får et
spektrum ut. Man kan gjerne gjøre en sammenhengende FFT på en
hel lydfil, men da vil utviklingen over tid inngå i spektral-
koeffisientene på en utydelig måte. Den svenske komponisten
Paul Pignon har arbeidet med slik "mammut-FFT", hvor han transformerer
en lydfil over i frekvensdomenet og spiller av spekteret som
samples direkte (!). Denne sammenblandingen av tids- og frekvensdomenet
er verdt å høre på, forunderlig nok.
En analysemetode som bedre følger hvordan øret og hjernen oppfatter
lyd, er korttids-FFT. Man tar da en spektralanalyse av korte biter
av lyden av gangen, slik at man får en rekke påfølgende
øyeblikksbilder av spekteret som varierer over tid. Vi må da velge
hvor mange punkter vi vil ha i FFT'en, dvs. hvor mange samples vi
vil analysere av gangen. Antall punkter betegnes oftest med bokstaven N.
De fleste FFT-algoritmer fungerer mest effektivt
hvis N er en potens av 2. Typiske verdier som brukes er
256 ( 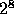 ), 512 (
), 512 ( 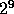 ), 1024 (
), 1024 ( 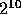 ) og 2048 (
) og 2048 ( 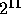 ).
Ut fra spektralanalysen vil vi da få N/2 verdier for amplityde og
fase for de N/2 frekvensområdene (kanalene) som er
jevnt spredt fra 0 Hz til Nyquist-frekvensen. Vi ser da at vi får
N tall ut til sammen, og vi puttet N tall inn. Spektralanalysen
har hverken skapt eller fjernet informasjon.
).
Ut fra spektralanalysen vil vi da få N/2 verdier for amplityde og
fase for de N/2 frekvensområdene (kanalene) som er
jevnt spredt fra 0 Hz til Nyquist-frekvensen. Vi ser da at vi får
N tall ut til sammen, og vi puttet N tall inn. Spektralanalysen
har hverken skapt eller fjernet informasjon.
Vi ser at jo flere punkter vi har i FFT'en, jo større oppløsning
får vi i frekvensdomenet (vi får flere "samples" i spekteret).
Med en samplingfrekvens på 32 kHz, vil N=512 gi en oppløsning
på 64 Hz, mens N=1024 vil gi en oppløsning på 32 Hz.
Men når vi øker N må vi analysere stadig lengre lydbiter,
og det gjør at vi får en dårligere oppløsning i tid.
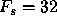 kHz og N=512 vil gi 64 spektre i sekundet (hver lydbit blir
16 ms lang), mens N=1024 vil gi 32 spektre i sekundet, så hver lydbit
blir 31 ms lang.
kHz og N=512 vil gi 64 spektre i sekundet (hver lydbit blir
16 ms lang), mens N=1024 vil gi 32 spektre i sekundet, så hver lydbit
blir 31 ms lang.
Vi får dermed en avveining mellom presisjon i frekvens og presisjon i
tid: Jo høyere nøyaktighet vi måler frekvensen med, jo lavere
nøyaktighet må vi nødvendigvis måle tiden med. I figurene under
er det vist hvordan vi kan dele opp frekvens-tid-planet på ulike
måter ved å justere N. Vi kan ikke plassere en hendelse i
tid og frekvens med større nøyaktighet enn en boks. Disse boksene
har alltid samme areal, slik at hvis vi øker nøyaktigheten i
frekvens (boksene blir lavere) minsker nøyaktigheten i tid (boksene blir
bredere) .
.

Figure 5.24: N=1 gir best mulig presisjon i tid, men gir
ingen frekvensinformasjon

Figure 5.25: 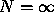 gir best mulig presisjon i frekvens, men gir
ingen plassering i tid
gir best mulig presisjon i frekvens, men gir
ingen plassering i tid
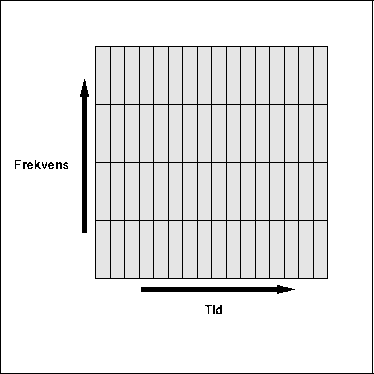
Figure 5.26: Liten N gir god presisjon i tid, men dårlig
presisjon i frekvens
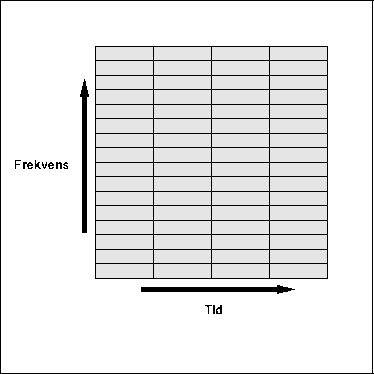
Figure 5.27: Stor N gir god presisjon i frekvens, men dårlig
presisjon i tid
Bestemmelse av N bør gjøres i hvert enkelt tilfelle, avhengig
av lyden vi arbeider med. Et stort antall tette frekvenskomponenter
kombinert med lave krav til presisjon i tid (langsom dynamikk), vil
typisk kreve store N. Færre frekvenskomponenter kombinert med
hurtige attacks krever typisk små N. Vi ønsker generelt å
sette N så liten som mulig for å få best mulig temporal
oppløsning, men ikke så liten at frekvensområdene gaper over
mer enn en deltone i lyden.
Vi vil imidlertid aldri miste informasjon i en FFT. Lyden kan derfor
rekonstrueres perfekt uansett N, så lenge vi ikke har gjort
noen endringer i spekteret.
De små områdene vi analyserer av gangen i en korttids-FFT
kalles vinduer. Av tekniske grunner (undertrykking av sidebånd
etc.) vil man vanligvis legge på en liten envelope på hvert av
disse vinduene før man utfører FFT'en. En slik envelope kalles en
vindusfunksjon, og det finnes mange ulike slike funksjoner, med navn
som Hamming, Hanning, Kaiser, Bartlett etc. Hver av disse har sine fordeler
og ulemper.
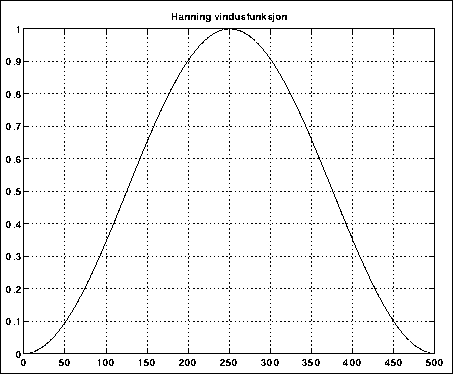
Figure 5.28: Hanning vindusfunksjon
For ikke å miste informasjon i overgangen mellom
vinduene, er det nødvendig å la dem overlappe. Denne
overlappingen er gjerne ganske drastisk, og derfor vil vi få ut
mange flere spektre pr. sekund enn vi så på over (uten at
oppløsningen i tid dermed blir noe bedre, vi får bare en
slags interpolering). Datamengden bli derfor stor ut fra en korttids-FFT.
Når vi nå har representert lyden i frekvensdomenet, åpner
det seg en verden av morsomme lydbehandlingsteknikker. Vi har allerede
nevnt hvor lett det er å lage filtre. Noen andre eksempler:
- Hvis vi adderer en fast verdi til hver frekvens, vil vi få et
spektralskift som vil introdusere inharmonisitet. Dette
tilsvarer på et vis en ringmodulasjon, bortsett fra at vi
får ett sidebånd, ikke to.
- Hvis vi multipliserer hver frekvens med en fast verdi, får vi
et pitch-skift uten medfølgende hastighetsendring. Dette er en
metode for harmonizing som gir meget god kvalitet.
- Vi kan snu spekteret opp-ned, slik at grunntonen blir den
høyeste harmoniske i spekteret og omvendt, eller permutere
deltonene på andre måter.
- Vi kan sortere deltonene etter amplityde, og beholde bare de
kraftigste.
- Vi kan filtrere spekteret, enten langs frekvensaksen (vil
framheve eller dempe bratte flanker i hvert korttidsspektrum)
eller langs tidsaksen (vil framheve eller dempe endringer i
klangen over tid).
- Vi kan analysere to lyder, og f.eks. multiplisere spektrene
med hverandre eller lage glidende overganger mellom dem på
forskjellige måter ("morfing").
- Vi kan tvinge deltonene henimot visse frekvenser, f.eks. en
musikalsk skala.
Her er det fritt fram for fantasien! Parametrene til disse metodene kan
selvsagt variere over tid.
Etter at vi har vrengt spekteret på en eller annen fantastisk
måte, er vi nødt til å komme oss tilbake til tidsdomenet
før vi kan høre lyden. Dette kalles resyntese, og er
egentlig bare en additiv syntese. Denne resyntesen kan gjøres med
den samme algoritmen som FFT, men med et par små endringer som
gjør at den virker baklengs. Dette heter invers FFT
(IFFT).
Enkelte ganger kan det være fordelaktig å resyntetisere lyden
med "rå makt", dvs. addere et stort
antall sinustoner direkte. Dette er langt mer tidkrevende enn IFFT.
Hvis vi strekker oppdateringen av parametrene i resyntesen utover i tid,
får vi en time-stretch (kompresjon/dilatasjon) av høy kvalitet uten
medfølgende pitch-endring.
Det ble nevnt at tallene som kommer ut av en FFT er amplityde og fase
for den deltonen som ligger innenfor hvert frekvensområde.
 Men musikere er nok mer opptatt av frekvens enn av fase. Derfor
benyttes ofte en teknikk som heter fase-vokoding, der
faseinformasjonen fra FFT'en brukes til å beregne frekvens. Dette
baserer seg på at endringen i fase fra analysevindu til analysevindu
er proporsjonal med deltonens frekvens. Vi får da ut eksakte
frekvenser, ikke bare informasjon om at deltonen ligger innenfor en
bestemt kanal.
Men musikere er nok mer opptatt av frekvens enn av fase. Derfor
benyttes ofte en teknikk som heter fase-vokoding, der
faseinformasjonen fra FFT'en brukes til å beregne frekvens. Dette
baserer seg på at endringen i fase fra analysevindu til analysevindu
er proporsjonal med deltonens frekvens. Vi får da ut eksakte
frekvenser, ikke bare informasjon om at deltonen ligger innenfor en
bestemt kanal.
Musikkprogrammet C-Sound har en fasevokoder, og den finnes også
i SoundHack for Mac og flere andre systemer. Fasevokoderen er brukt
i mange musikkstykker til mange forskjellige formål.
Menneskets tale fungerer ved at stemmebåndene produserer et pulstog
med et nokså flatt spektrum. Dette pulstoget filtreres videre av
hals og munnhule. Forskjellige vokaler tilsvarer forskjellige
frekvenskarakteristikker for dette filteret. Et typisk trekk ved disse
karakteristikkene er to eller flere tydelige resonanser (formanter).
Ved lineær prediksjon forsøker vi å produsere et filter av
differenslikning-typen, med koeffisienter som varierer over tid.
Dette filteret skal etterlikne filterkarakteristikken til lyden vi
analyserer. Signalet kan siden re-syntetiseres ved å eksitere
filteret med et syntetisk pulstog som etterlikner stemmebåndene.
Vi kan på den måten kode tale bare gjennom filterkoeffisientene,
som varierer forholdsvis langsomt, og dermed har vi en effektiv metode
for data-reduksjon av talesignaler. Lineær-prediktiv koding (LPC) har
oppnådd en posisjon innen talesyntese, selv om lydkvaliteten ofte
er dårlig (dette bunner i bruk av for få filterkoeffisienter,
og stiliseringen av eksitator). Den typiske "robot-stemmen" som var vanlig
i tale-synthesizere for noen år siden, var produsert ved hjelp av LPC.
Som vi har sett, kan eksitator-resonator-modellen anvendes på de fleste
musikkinstrumenter. LPC begrenser seg derfor ikke til bruk på tale.
LPC kan brukes til å vri lyden på mange rare måter. Vi kan
f.eks. variere pitch ved å skru på frekvensen til eksitator.
I vanlige harmonizere, og i pitch-skift med FFT, vil formantenes posisjon
endre seg. Tale fungerer ikke på den måten, og LPC gir derfor
et mer korrekt resultat, uten den typiske "Donald-stemmen".
Vi kan også kjøre andre lyder gjennom filteret vi har generert.
På den måten kan vi gjøre kryss-syntese, f.eks. ved at vi
simulerer at vi har et symfoniorkester plassert i strupehodet istedenfor
stemmebånd. Vi får da et "talende orkester".
Det må innrømmes at LPC ofte ikke låter så bra. Det krever
erfaring å utnytte LPC på den beste måten, bestemme hvor mange
filterkoeffisienter vi skal ta med etc.
Guruen innenfor musikalske anvendelser av LPC er den amerikanske komponisten
Paul Lansky. Musikkprogrammet C-Sound inneholder en implementasjon av LPC.
Det finnes en annen metode for spektralanalyse som kanskje er lettere å
begripe, men som ikke er så beregningseffektiv som FFT, nemlig bruk av
en filterbank. En filterbank er en bunke med båndpassfiltre
koblet i parallell, med senterfrekvenser som er spredt over hele
frekvensområdet. Det gjøres en RMS-analyse eller annen type
energi-analyse på output fra hvert filter, og dermed får vi
informasjon om hvor mye energi vi har innenfor hvert frekvensbånd.
Filterbanker er historisk viktige, fordi de kan implementeres analogt.
De fleste enkle spektralanalysatorer av den typen vi finner i lydstudioer,
fancy stereoanlegg etc. benytter filterbanker. Den klassiske effektboksen
som kalles "vokoder" har en filterbank koblet sammen med en oscillatorbank.
Dette gir en enkel form for analyse-resyntese.
I de senere år har filterbanker fått en kraftig renessanse. Man
har begynt å sette pris på kontinuiteten som filterbanker
gir i forhold til den mer opphakkede, vindusbaserte FFT-metodikken.
Samtidig har digitale signalprosessorer blitt raske nok til å
benytte filterbanker i sann tid. De nye digitale kompakt-kassettene
(DCC), og Minidisc, benytter filterbanker som en del av datakompresjonen.




Next: Granulære metoder
Up: Digital lydbehandling
Previous: Fysisk modellering
\yvind Hammer
Fri Feb 21 21:39:51 MET 1997











