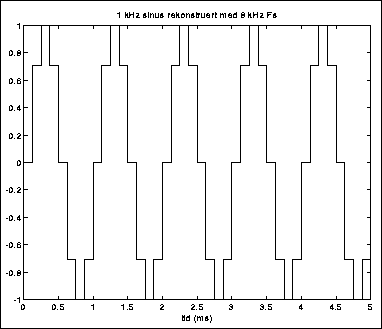
Figure 4.6: Utgang fra D/A-omformeren
Nå er altså signalet samplet og lagret digitalt, en tallverdi for hver måling. I dette avsnittet skal vi se på hvordan tallverdiene kan omformes tilbake til et analogt signal. Dette kalles rekonstruksjon, og er den omvendte prosess av sampling. En digital/analog-omformer (D/A-omformer) står sentralt i denne prosessen.
En D/A-omformer produserer en spenning på grunnlag av en digital verdi som blir sendt ut fra datamaskinen. For å rekonstruere et analogt signal ut fra digitale verdier, kan vi således sende sekvensen av verdier ut på D/A-omformeren med samme hastighet som signalet ble samplet med. Hvis vi har samplingfrekvens 30 kHz, må vi sende 30 000 tallverdier ut på D/A-omformeren hvert sekund. Vi kan også endre denne hastigheten, med hastighets- og pitch-endring som resultat.
Figur 4.6 viser utgangen fra D/A-omformeren når vi sender ut sekvensen som vi fikk da vi samplet en 1 kHz sinus med 8 kHz samplingfrekvens. Tatt i betraktning at det originale, analoge signalet var en ren sinus, ser jo dette ut som et nokså mislykket resultat. Akustisk vil den "firkantede" formen arte seg som masse bråk og ringing fra Nyquist-frekvensen (her 4 kHz) og oppover.

Figure 4.6: Utgang fra D/A-omformeren
Ved å betrakte samplingsprosessen som modulasjon med et tog av enhetsimpulser, kan man vise at dette bråket er speilinger av det originale spekteret om Nyquist-frekvensen og heltallsmultipla av denne. For de som måtte ha glede av det, kan dette formaliseres ved at den Fourier-transformerte av signalet x modulert med toget av forsinkede Dirac-impulser er konvolusjonen av den Fourier-transformerte av x med et tilsvarende tog i frekvensdomenet:
![]()
Det originale spekteret er altså intakt, men har fått masse
uønskede komponenter i tillegg, fra Nyquist-frekvensen og oppover.
Disse komponentene kan fjernes ved hjelp av et skarpt lavpassfilter,
som klipper like under Nyquist-frekvensen. Dette filteret kalles et
rekonstruksjonsfilter. Etter rekonstruksjonsfilteret skal
signalet i prinsippet være perfekt rekonstruert. Trappetrinnene
i figuren over vil da være fjernet, og vi vil ha en perfekt sinus
igjen. Dette er egentlig et litt merkelig (og for oss svært heldig)
resultat
![]() .
.
Det komplette samplings- og rekonstruksjons-systemet er vist i figur 4.7. Det analoge signalet lavpassfiltreres i antialiaseringsfilteret, slik at vi sikrer oss mot aliasering. Signalet samples og måles så i A/D-omformeren, og lagres og/eller behandles i et digitalt system (datamaskin). Tallverdiene sendes videre ut til D/A-omformeren, som produserer en trappetrinn- aktig versjon av det analoge signalet. Trappetrinnene fjernes så i rekonstruksjonsfilteret.

Figure 4.7: Komplett system for sampling og rekonstruksjon