Figure: 1 kHz sinusoid samplet med 8 kHz
En grunnleggende regel i samplingsteorien er at samplingfrekvensen må være mer enn dobbelt så høy som den høyeste frekvenskomponenten vi ønsker å kunne registrere. Sagt omvendt: Den høyeste frekvenskomponenten vi kan registrere er mindre enn halve samplingfrekvensen. Dette er en del av Shannon og Nyquist's samplingsteorem. Halvparten av samplingfrekvensen kalles Nyquist-frekvensen. Vi skal ikke teoretisere for mye rundt samplingsteoremet, men illustrere det ved et eksempel. Dette eksemplet vil også demonstrere det fryktede aliaserings-fenomenet.
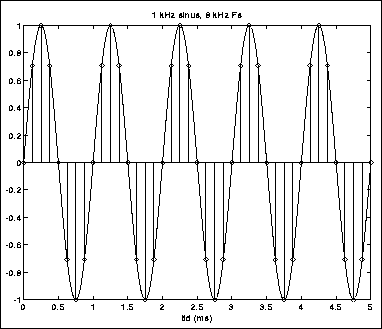
Figur 4.1 viser et analogt, sinusformet signal, la oss si med frekvens 1 kHz (1000 Hz). Vi ønsker å sample dette signalet, dvs. måle momentanverdien med jevne mellomrom. Figuren viser signalet samplet med 8 kHz samplingfrekvens. De målte verdiene vises ved hjelp av stolper. Vi ser at signalet er godt registrert.

Figure: 1 kHz sinusoid samplet med 8 kHz
I figur 4.2 går vi ned til 4 kHz samplingfrekvens. Signalet er fremdeles registrert.
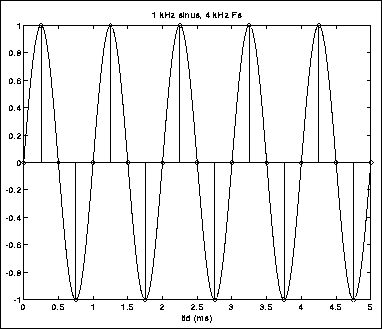
Figure: 1 kHz sinusoid samplet med 4 kHz
I figur 4.3 sampler vi med 3 kHz, signalet er fremdeles registrert.
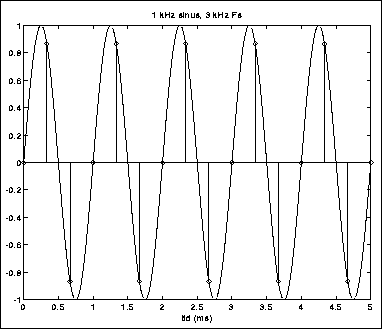
Figure: 1 kHz sinusoid samplet med 3 kHz
Så går vi helt ned til 2 kHz samplingfrekvens (figur 4.4). Vi ser at det går dårlig. I dette spesielle tilfellet er vi så uheldige å sample akkurat i nullgjennomgangene, og vi får ikke ut noen ting.
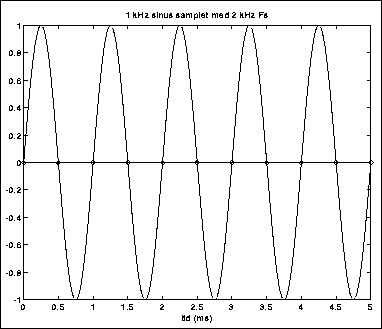
Figure: 1 kHz sinusoid samplet med 2 kHz
En samplingfrekvens på 3 kHz er altså tilstrekkelig for å registrere en frekvenskomponent på 1 kHz, mens 2 kHz blir for lite. Dette stemmer med samplingsteoremet.
La oss så forsøke å senke samplingfrekvensen ytterligere. I figur 4.5 sampler vi med 1500 Hz. Det samplede signalet beskriver nå en sinustone på bare 500 Hz (stiplet linje).
Signalet på 1000 Hz er altså blitt feilregistrert som et signal på 500 Hz. Med andre ord blir signaler som ligger over halve samplingfrekvensen foldet (speilet) nedover i spekteret, og danner falske frekvenser. Dette er et alvorlig problem i digital lyd, som kalles aliasering. Vi tar det en gang til:
Aliasering er et fenomen som kan oppstå i en samplingsprosess, dersom signalet vi sampler inneholder frekvenskomponenter over halve samplingfrekvensen. Disse komponentene speiles nedover i spekteret og danner falske frekvenser.
Bemerk at "samplet signal" også inbefatter signaler som er beregnet ved en matematisk metode internt i en datamaskin. Under beregningene må vi alltid passe på at signalet ikke inneholder komponenter over halve samplingfrekvensen. Disse vil forårsake aliasering. Et enkelt forsøk på en FM-synthesizer (DX 7) vil demonstrere dette. Hent inn en lyd med et rikt spektrum, og spill den øverst på klaviaturet (bruk ev. Key Transpose for å komme enda høyere opp). De lyseste komponentene blir speilet nedover, og forvrenger lyden kraftig.
Når vi skal sample en lyd, må vi altså passe på at signalet er så båndbreddebegrenset at aliasering unngås. For å sikre dette, er det vanlig å sette et lavpassfilter før A/D-omformeren, et såkalt antialiaseringsfilter. Antialiaseringsfilteret må være så skarpt som mulig, og klippe like under halve samplingfrekvensen.