I analoge synthesizere benyttes spenningsstyrte forsterkere (VCA) til å endre amplityden til en lyd. En varierende kontrollspenning styrer da amplityden til lyden som passerer gjennom VCA'en, og vi sier at lyden amplitydemoduleres av kontrollsignalet (modulatoren).
I den digitale verdenen gjør vi dette ved å multiplisere hver av sample-verdiene i lyden med tilsvarende samples i kontrollsignalet. Hvis vi multipliserer med en konstant, vil hele lyden endre amplityde uniformt. Multiplikasjon med 0 gir total dempning, multiplikasjon med 0.5 gir 6 dB dempning, 1.0 endrer ikke amplityden, 2.0 gir 6 dB forsterking.
Ved å endre kontrollsignalet over tid, kan vi lage envelopes. Siden øret ikke kan oppfatte hurtige styrkevariasjoner, er det mulig å benytte en lav samplingfrekvens i envelopetabellen, kanskje under 1 kHz. I programmet C-Sound gjøres dette ofte for å spare beregningstid. Det kan da imidlertid ofte oppstå klikk. Den ideelle løsningen er kanskje å bruke en liten envelope-tabell, men å interpolere mellom samplene i kontrollsignalet.
Hvis vi modulerer med en sinustone, får vi ringmodulasjon.
Hvis vi modulerer med en sinustone med frekvens 
, vil hver av
deltonene i lydspekteret forsvinne. I stedet får vi to nye deltoner,
med avstand 
fra den opprinnelige deltonen og med halve
amplityden. Disse deltonene kalles sidebånd.
Som vi forklarte i heftet om akustikk, kan dette vises ved
hjelp av formelen for multiplikasjon av to sinusoider:
Figur 5.1 demonstrerer dette.
Den opprinnelige frekvenskomponenten på 400 Hz er her utsatt for ringmodulering med modulatorfrekvens 100 Hz. Vi har da fått sidebånd på 300 Hz og 500 Hz.
Ringmodulasjon er en "klassisk" metode for lydomforming som ble mye brukt særlig på 50- og 60-tallet (Stockhausen, Nordheim etc.).
Miksing av digital lyd skjer simpelthen ved at man adderer korresponderende sample-verdier. Dette krever at alle lydene er samplet med samme frekvens. Akkurat som i analog lyd må man passe på at summen holder seg innenfor maskinens dynamiske område, ellers får man klipping.
Når vi mikser vil vi gjerne fade ting inn og ut. Dette gjøres ved å legge på envelopes på hver lyd før addisjonen.
Den enkleste metode for lydsyntese er at brukeren simpelthen angir kurveformen direkte som et oscillogram. Kurven kan tegnes med et tegneverktøy på skjermen, eller genereres ved en angitt matematisk funksjon. Den vanligste metoden er å legge en periode av kurven inn i en tabell med opptil noen få tusen samples. Denne tabellen presses eller strekkes automatisk, avhengig av hvilken grunntonefrekvens vi ønsker, og så gjentas (loopes) denne perioden så lenge vi vil. Vi kan siden legge på envelopes eller behandle lyden ved andre omformingsmetoder.
Et lite problem ved kurveform-syntese (og generelt i digital lyd) er
interpolasjonsstøy. Anta for eksempel at vi har en kurvetabell med 100
samples, og at samplingfrekvensen er 20 kHz. Dersom tabellen avspilles som
den er, vil det ta 
sekunder å spille en
periode, hvilket gir en grunntonefrekvens på 200 Hz. Hvis vi nå
ønsker en grunntonefrekvens på 300 Hz, må vi gå gjennom
tabellen med en hastighet på 1.5 ganger det "normale". Måten å
gjøre dette på, er å plukke ut hvert 1.5'te sample for avspilling.
I praksis må da synteseprogrammet enten bare hente det nærmeste
samplet i tabellen, eller man må interpolere. Slik interpolasjon er
aldri perfekt, og dermed får vi støy.
Interpolasjonsstøy kan minimaliseres på to måter: Enten benytte en større kurveformtabell, eller benytte en bedre (og dermed mer beregningskrevende) interpolasjonsmetode. Vi får dermed en avveining mellom hukommelsesbruk, regnehastighet og lydkvalitet.
Kurveform-syntese er morsomt og lærerikt, fordi en lyd kan tegnes helt direkte. Med litt øvelse kan man også oppnå mange spennende effekter. Men øret oppfatter nå engang lyden i frekvensdomenet, slik at det ofte kan være vanskelig å forutsi hvordan en lyd som er angitt i tidsdomenet vil klinge. Dessuten kan det være kronglete å oppnå dynamikk i klangfarge.
Kurveform-syntese er en metode som har vært kommersielt populær, under navn som "PCM-syntese" (Casio) og "Waveform Synthesis" (Korg).
Additiv syntese går simpelthen ut på at brukeren angir spekteret direkte, enten statisk eller varierende over tid. Datamaskinens oppgave er så å omforme lyden fra frekvensdomenet til tidsdomenet. Fra Fourier's teorem følger det at enhver kurveform kan syntetiseres ved hjelp av additiv syntese. Kommunikasjonen med brukeren foregår dessuten i frekvensdomenet, som er den samme representasjonsform som øret benytter. Dette gjør additiv syntese til en meget kraftig metode, bortsett fra at antall parametre (amplityde og frekvens til hver av deltonene) kan virke litt overveldende. Ofte vil imidlertid disse parametrene ha sitt grunnlag i en foregående, maskinell spektralanalyse av en samplet lyd. Vi skal komme mer tilbake til slik analyse-resyntese.
Additiv syntese kan være en nokså beregningskrevende sak, fordi man skal regne ut et stort antall sinusoider med varierende amplityde og mikse disse sammen. En alternativ og langt hurtigere beregningsmetode er å bruke invers Fast Fourier-transformasjon (IFFT). Dette kommer vi også tilbake til.
Det finnes et antall kommersielle synthesizere som benytter additiv syntese (f.eks. fra Kawai).
FM-syntese er kanskje den mest populære digitale syntesemetoden, ikke minst på grunn av Yamahas DX7-serie. FM er en indirekte og lite intuitiv teknikk. Det krever øvelse å kunne bestemme synteseparametrene riktig for å få en ønsket lyd. Grunnen til denne metodens popularitet er først og fremst at den kan produsere forholdsvis komplekse klanger uten at datamaskinen behøver å slite for mye. Det var amerikaneren John Chowning som først pekte på FM-syntese som musikalsk verktøy.
Som en introduksjon til FM kan vi betrakte et oppsett som lager sinustoner med vibrato. Vi benytter to sinusoscillatorer: En oscillator C som lager selve lyden, og en lavfrekvent oscillator (LFO) M som styrer frekvensen til C. Dette kan tegnes slik:
I FM-sjargong kalles M for modulator, og C for carrier.
Frekvensen som M svinger med kalles modulatorfrekvensen, og
gjennomsnittsfrekvensen til C kalles carrierfrekvensen.
Amplityden til M heter modulasjonsindeks, og benevnes her med
bokstaven I. Amplityden til C spiller bare rolle for lydstyrken.
I dette systemet har vi dermed tre interessante parametre som kan endres:
Modulatorfrekvens, carrierfrekvens og modulasjonsindeks.
M svinger her med en lav frekvens, og vi får en vanlig sinus med vibrato. Dersom vi imidlertid øker frekvensen til modulator opp i det hørbare området, vil vi få kraftig endring av klangfargen. Hvilken klangfarge vi får, avhenger av forholdet mellom frekvensen til C og frekvensen til M (såkalt C:M ratio) og av modulasjonsindeksen.
Vi kan sette opp følgende "regler" for hvordan spekteret til ovenstående system er bygget opp:
I figurene 5.2-5.6 kan vi se hvordan spekteret blir rikere ettersom vi øker modulasjonsindeksen. Carrierfrekvensen er her så stor i forhold til modulatorfrekvensen at vi ikke får refleksjoner.
Det er fristende å vise dette i tre dimensjoner, selv om situasjonen kanskje blir litt utydelig (figur 5.7).
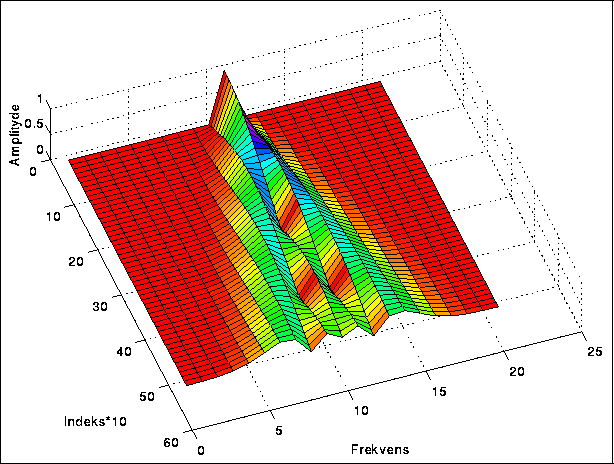
Figure 5.7: FM-spektrum med varierende indeks
Foreløpig har vi betraktet et system med bare to oscillatorer: En carrier og en modulator. Parametrene er dessuten statiske. I FM-syntese pleier vi imidlertid å bruke flere enn to oscillatorer. For å oppnå dynamikk i klangfarge, legger vi envelopes på modulatorene, og for å få dynamikk i styrke, legger vi envelopes på carrierne. Av dette følger en generell byggeblokk som kan brukes både som carrier og modulator, nemlig en oscillator med envelope på utgangen og med styrbar frekvens. En slik byggeblokk kalles en operator. DX7 har 6 slike operatorer, som kan kobles sammen på 32 forskjellige måter. En slik sammenkoblingsmåte (patch) kalles en algoritme. Her en noen eksempler på FM-algoritmer:
Algoritmen lengst til høyre er egentlig ikke FM-syntese, men en enkel additiv syntese med 6 deltoner.
Denne metoden heter på engelsk Non-linear Distortion, på fransk Distortion Non-Lineaire, forkortet DNL. Poenget er å kjøre lyd (sinustoner eller naturlig lyd) gjennom en ulineær overføringsfunksjon. Denne funksjonen kan f.eks. implementeres som en tabell der input-sampleverdien brukes som en indeks som peker ut en verdi i tabellen. Denne verdien blir output-verdi.
Overføringsfunksjonen kan tegnes på en dataskjerm, eller den kan beregnes matematisk. Enhver funksjon kan legges inn i tabellen. Her er noen eksempler (du finner flere i heftet om matematikk):
(identitetsfunksjonen) endrer ikke lyden i det hele tatt, fordi output-samplene f(x) er de samme som input-samplene x.
vil doble amplityden. Dette gir en forsterking på 6 dB. Disse to funksjonene er begge lineære; funksjonsgrafen er en rett linje. Dette betyr at klangfargen beholdes.
der abs(x) er absoluttverdien av x (fortegnet kastes) er en ulineær funksjon som endrer lydens klangfarge og gir en fuzz-aktig effekt.
Av spesiell interesse er en type overføringsfunksjoner som kalles Chebychev-polynomer. Disse polynomene har den interessante egenskap at dersom vi sender en sinustone gjennom dem, får vi en harmonisk ut. Et polynom av andre grad gir andre harmoniske, tredje grad gir tredje harmoniske osv. Ved å legge sammen flere polynomer, får vi et nytt polynom som kan produsere et helt spektrum når vi sender en sinustone gjennom det. Vi har da full kontroll over deltonenes amplityder. Dette forutsetter imidlertid at input-sinusen har amplityde 1. Ved mindre amplityder får vi et fattigere spektrum ut. På denne måten vil klangen endre seg (bli rikere og lysere) med større amplityde. En liknende oppførsel er kjent fra de fleste musikkinstrumenter.
Det bør nevnes at både kurveform-syntese og FM-syntese kan betraktes som spesialtilfeller av ulineær kurveforming. Dette er nok imidlertid mer av teoretisk enn av praktisk interesse.
RMS-analyse (Root-Mean-Square) er den klassiske måte å måle signalstyrke på. En signalstyrkemåler kan brukes til å trekke ut amplityde-envelopen til en lyd. Denne envelopen kan så endres eller anvendes på andre lyder. Dette siste er et enkelt eksempel på kryss-syntese, der man trekker ut informasjon fra en lyd og anvender på en annen.
Ved RMS-analyse kvadrerer vi først hvert sample. Dette gjør at vi bare får å gjøre med positive verdier i det følgende. Deretter integrerer vi (tar gjennomsnittet) over et visst tidsrom. Bemerk at dersom vi ikke hadde kvadrert til å begynne med ville enhver sinusoid integrere til null, og resultatet ville vært verdiløst. Til slutt trekker vi ut kvadratroten for å oppveie kvadreringen. Vi beregner altså kort sagt roten av gjennomsnittet av kvadratet, derav navnet RMS.
Det interessante spørsmålet her er hvordan og over hvilke tidsrom vi skal ta gjennomsnittet. Det finnes flere forskjellige måter å produsere et gjennomsnitt på:
Integrasjonstiden T bestemmer hvor nøye envelopen skal tracke lyden. Vi ønsker ikke at trackingen skal være for nøyaktig, for da kan vi risikere å begynne å følge selve kurveformen ved lavfrekvente signaler. På den annen side må T være såpass liten at transienter ikke dempes for mye. Dette er en vanskelig balansegang, og T bør helst settes manuelt ettersom hvaslags lyd man har med å gjøre.
Figurene 5.9-5.11 viser tre eksempler på RMS-måling med
løpende integrasjon, med ulike T. Testlyden er en sinustone med en skarp
attack (figur 5.8).
Tonen dør så ut samtidig med at frekvensen senkes.
Legg merke til hvordan transientresponsen, som observeres i begynnelsen
av signalet, blir dårligere ettersom vi øker T. Men samtidig
dempes selve signalet bedre ved de lave frekvensene på slutten.
T=32 er muligens et brukbart kompromiss.
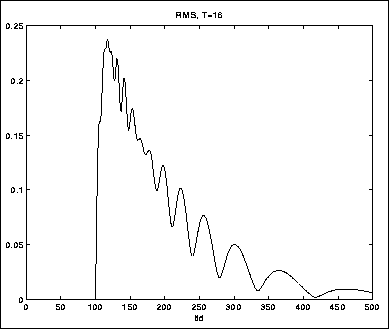
Figure 5.9: Glatting over 16 samples
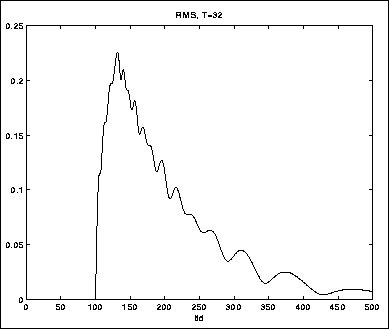
Figure 5.10: Glatting over 32 samples
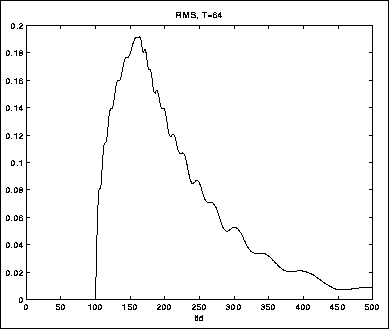
Figure 5.11: Glatting over 64 samples
Vi kan prøve etpar andre metoder også. Hvis vi velger ut den maksimale verdien i de siste 64 samples, får vi resultatet i figur 5.12.
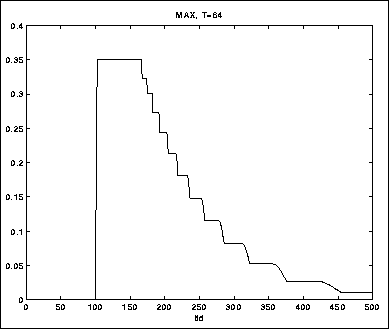
Figure 5.12: Envelope-tracking med max-filter
En annen teknikk er peak-deteksjon, det vil si at vi forsøker å finne toppene i kurven og trekker linjer mellom disse (figur 5.13).
Akkurat for denne lyden fikk vi her et glimrende resultat, men generelt vil denne metoden gå i vasken når vi begynner å få inn overtoner som lager "småtopper" mellom hovedtoppene. Det finnes imidlertid endel triks for å forsøke å overse disse.
En annen viktig analyse-teknikk er pitch-følging eller
-analyse, der vi forsøker å plukke ut grunntonefrekvensen
i et signal. Dette forutsetter naturligvis at vi har å gjøre med
en monofon lyd med en veldefinert grunntone.
Å finne frekvensen til en grunntone er en meget komplisert affære, og det er ikke klart hvordan øret og hjernen løser denne oppgaven. Et stort antall metoder er pønsket ut for pitch-følging, men ingen av dem er ufeilbarlige. En vanlig feil er at analysatoren plukker ut frekvensen til en overtone, slik at vi kan få f.eks. en pitch som ligger en oktav for høyt.
En klassisk teknikk er peak-deteksjon, der vi teller antall bølgetopper i sekundet. For å unngå å telle små-topper som stammer fra overtoner, kan vi gjøre en kraftig lavpassfiltrering først. Dette lavpassfilteret bør følge grunntonefrekvensen gjennom en feedback- mekanisme.
En liknende metode er å telle nullgjennomganger, dvs. de punktene der kurven går fra negative til positive verdier. Igjen vil overtoner kunne lage problemer, og vi bør lavpassfiltrere signalet først.
En av de smartere metodene går ut på å benytte et kamfilter som slipper gjennom en viss grunntonefrekvens og harmoniske av denne, men demper alle andre frekvenser. Et slikt filter er lett å lage. Grunntonefrekvensen varieres så inntil vi finner et maksimum i signalstyrken ut fra filteret. Vi kan da regne med at toppene i filterkarakteristikken har truffet deltonene i det opprinnelige signalet. Ettersom pitch varierer, passer vi på å oppdatere filteret slik at signalstyrken forblir størst mulig. En slik algoritme kan bli lurt ved at den stabiliserer seg på en subharmonisk. Hvis vi har en grunntonefrekvens på 300 Hz, kan vi risikere at analysatoren finner et maksimum for 100 Hz, fordi topp nr. 3, 6, 9 etc. i kamfilteret treffer deltonene på 300 Hz, 600 Hz, 900 Hz etc. Man bør derfor forsøke å finne den største frekvensen som gir maksimum.
Det finnes også metoder som arbeider i frekvensdomenet, ved at man gjør en spektralanalyse og finner toppene i spekteret. Grunntonefrekvensen bestemmes så som største felles faktor av disse toppene.
